One should not think slightingly of the paradoxical; for the paradox is the source
of the thinker's passion, and the thinker without a paradox is like a lover without
a feeling: a paltry mediocrity.... The supreme paradox of all thought is the
attempt to discover something that thought cannot think.
the Danish theologian and philosopher Søren Kierkegaard (1813-1855)
Thought is only a flash between two long nights, but this flash is everything.
the French mathematician Henri Poincaré (1854-1912)
What am I, that I can think about my existence?
the American neurophysiologist Rodolfo Llinás, 1986
The century-old school on School Street is a National Historic Something too, and a bit more
likely to survive the winter storms than the Outermost House. It is perched on the highest bank
surrounding Eel Pond and protected from the winds off Vineyard Sound by an even higher hill, a
site selected by someone who had longevity in mind. Its playground has a basketball hoop, and
the children are practicing their free throws for a few minutes as they take their recess from the
Children's School of Science.
The adults around here like to throw as well -- there's a game of Frisbee in the street and the
softball teams are practicing at the ball field, which is a block behind the Bell Tower Garden, and
surrounded by the remains of the original saltwater marsh. Home runs may disappear into a
thicket penetrable only by small boys and girls -- or, worse yet, into a thicket that admits only
small mammals. The volleyball court is right next to the brambles; I played several games with
the computational neuroscience course students the other day, and we soon learned the penalties
of wild returns.
We also got some training from an old pro, who must have trained visiting students for many
seasons. All around town, you see beggar dogs, each the proprietor of a tennis ball lying on the
ground in front of them. They are, however, well fed. Their eager eyes are soliciting humans:
Please throw my ball! The old white dog by the volleyball court waits patiently by the edge of
the court, watching the game with his tennis ball nearby. Periodically, one of the players will,
without prompting, walk over and throw the dog's tennis ball toward the softball field, as far
away as possible, and the dog will happily chase it, returning to wait alongside the volleyball
court again. It seems to be a local tradition.
If five minutes goes by without someone helping out the dog, he will carry his ball onto the
volleyball court, wag his tail somewhat sheepishly, and generally disrupt the game until someone
gets rid of him by throwing his ball. It is quite clear who has trained whom; a little operant
conditioning works wonders on humans.
It is amazing how many entertainments around here involve ballistic movements: throwing,
clubbing, as in golf and tennis, kicking in soccer -- even the accurate bouncing used in
volleyball. Hammering is a favorite pastime, judging from the do-it-yourself types busy adding
something on to a porch or repairing a roof. Wonder why so many pastimes are so jerky? And if
they're not jerky, they are still fancy finger sequences such as cat-in-the-cradle or knitting. Is this
thanks to our ancient heritage of toolmaking, or cracking nuts? Or are they all secondary to
something even more basic?
THE SHINING SEA BIKEWAY is more crowded today; besides the usual bikes, I see a
recumbent. And the only permitted motorized vehicle, an electric wheelchair. Soon the beach
comes into sight, and it is a stony beach. The bathing beaches closer to Woods Hole used to be
stony as well, back before sand was imported. Of course, sand is always imported; very little of
it is made at the beach (the exceptions are those black sand beaches in Hawaii, the fine particles
formed when hot lava shattered as it dropped into the cold ocean). Ordinary sand comes from
weather eroding mountains, the long downhill trip breaking rocks into smaller and smaller
pieces.
I like stones -- you can't throw sand, at least not with a satisfactory feeling of accomplishment.
These stones, left behind by the glacier that plowed Cape Cod into place, are just the kind to fit
the hand of a child. But I know where to find the larger ones that will fit my hand: usually
farther along the beach from where the small stones are, because the ocean currents sweep along
parallel to this shore and carry the small, light ones farther than the heavier large stones. Double
the size of a stone and its surface area increases four-fold; you might think that more "sail" area
would cause the stone to be carried further by a wave but this is another surface-to-volume ratio
phenomenon: The stone's weight (which is proportional to its volume) goes up eight-fold! So
"move-ability" halves when size doubles. That is, of course, why the imported sand gets carried
away from stony beaches: They're stony because they have strong currents sweeping along the
shoreline that sort by size. And sand is easy stuff to move for such currents.
Whole beaches full of rocks like this are called shingle, at least by the British, who are thought to
have borrowed the term from the Norwegians. There is no shade anywhere. Some people are not
very fond of it:
Three or four times in my life I have ventured for a weekend to Martha's Vineyard,
Wellfleet or some other nesting place of the weary literate. The need to engage in
seemingly intelligent conversation while sitting under the hot sun, on hot sand,
while eating sand-impregnated hamburgers and watching the remnants of
someone's lunch of last week ooze up through the shingle must be one of life's most
starkly negative pleasures. Always I've re-achieved civilization with relief.
the economist John Kenneth Galbraith, 1981
Maybe I'll have to start a Cobble Appreciation Society (individually, the shingle's rounded rocks
are called cobbles); after all, even the ancient Greeks may have had one, since there is some
suggestion that a cobble was then called a discus (scholars argue about whether the word, as used
in Homer, means the same thing as the platter that athletes throw these days). A compromise
would be that discus meant a rock particularly suitable for throwing: One that fit the human hand
or that had nice aerodynamics.
Nothing feels quite as comfortable in the hand as a nice cobble: Have you ever hefted a hammer,
or pen, or club that felt quite so much like it was a natural extension of you, that one had been
designed to fit the other? The cobble's use as a hammerstone might explain the origins of the
term cobbler, with its unsophisticated connotations.
Dogs won't usually fetch stones, unfortunately, and so those with canine companions search out
the sticks and forlorn tennis balls that dogs prefer to chase. The problem with training a young
dog to fetch is not in getting him to chase and find the stick, nor to bring it back: The problem is
the war of wills needed to get him to give it back to you so that you can throw it again. That's a
familiar story to the biologists who study the structure of the fancy folded molecule that carries
oxygen from your lungs to your brain: The problem is not so much in getting a molecule to
snatch up oxygen and bind it, but in getting it to drop oxygen on command when arriving at the
tissues that need some. That is the genius of hemoglobin.
Yet another ballistic pastime to add to the list of discus throw, baseball, basketball, soccer, home-repair hammering, volleyball, and the like, which I've seen today: the game of fetch. I cannot
think of any other animals that enjoy so many ballistic entertainments, though juvenile apes
clearly love to "play hammer," especially if their elders make a living by cracking nuts. Even
infant chimps have been observed to hammer on a nut with a stick. And their elders sometimes
use rocks as hammers when trying to crack particularly tough nutshells.
ONCE YOUR BRAIN has the neural machinery for one ballistic movement, maybe it can be
used for another. Maybe the neurons used to command a hammering motion can be used with
the leg muscles too, and so kicking comes along for free. Certainly, any ballistic movement
requires a lot of neural machinery for planning ahead, quite unlike other movements, such as
walking or picking fruit off a tree. That's because ballistic movements are so fast, and our
feedback pathways are relatively slow. When a monkey moves a cherry from tree to mouth, or I
pick up a coffee cup and bring it to my lips, there is a lot of time for little corrections. The
sensors in my arm muscles and joints tell my spinal cord and brain where the cup is (they don't
speak directly to the local muscles, only via the loop into the central nervous system), I compare
that to my intent (cup at lips, preferably still upright) and known constraints (don't slosh the
coffee out of the cup), and correct the path. I repeat this correction dozens, if not hundreds, of
times during the seemingly smooth movement.
Still, each correction takes time because the message moves slowly along the nerves, and the
central nervous system takes time to decide too. A minimum round-trip loop time for arm-back-to-arm movements in humans is 110 milliseconds. And so, any movement like hammering or
kicking that may be over and done with in a fraction of a second cannot profit from corrections
along the way (dart throwing takes about 119 milliseconds until you release). Most error
corrections will arrive too late to do any good, as the motion will be complete by then. Maybe
you can use the feedback to help in your planning for the next throw, but once you start a throw,
you're committed to the plan you made during "get set."
I've been practicing juggling with several old, waterlogged tennis balls that I found. Oranges are
better for juggling than tennis balls, due to their weight, but I'm fresh out of oranges. Juggling is
hard in the beginning because of the reaction time between seeing a ball and generating a
correction nearly a fifth of a second later (visual reaction times are particularly slow). When
juggling, you've got to plan several movements ahead, not just one. And that is one reason why
it is so hard to learn.
This makes ballistic movements quite unlike the ones where an intention and feedback-corrections suffice to get the job done: Brief movements have to be carefully planned in
advance. Any trial and error has to be done while planning, checking a proposed movement
against memory as you "get set," and discarding the plans that don't jibe. Of course, a standard
kick, like the standard basketball free throw, may only require that the brain have a standard
motor program that it can execute on command; you make it standard by "getting it in the
groove" with long practice. It is when there is an infinite variety of gradations that planning
becomes so important, as you have to generate a number of possible sets of muscle commands
and then pick and choose to find the best one. That's why well-practiced free throws are easier
than other shots in basketball, which are from a variety of distances and angles. So guess which
were likely the ones important in evolution, needed by those prehuman hunters...?
The planning process probably requires a holding queue, what in the business we would call a
serial buffer. Telephones that remember your ten most-used numbers have ten serial buffers,
each more than a dozen digits long. Each is like a sidetrack, whose train sits poised, waiting to
be selected and let loose on the main line.
That which we call linking of ideas in our understanding is only the memory of
the coexistence of phenomena in nature; that which we call consequence in our
understanding is nothing but the memory of the sequence of succession of effects
in nature.
the French philosopher Denis Diderot (1713-1784)
FOR ORGANISMS THAT NEED TO BE both large (meters of conduction distance) and fast,
one often needs a queue that is the neural equivalent of an old-fashioned roll for a player piano.
It's a plan for many simultaneous output channels (those eighty-eight keys), which says when,
how hard, and for how long each of them is to be struck.
Our planning queue for a ballistic movement has to provide for dozens of muscles and activate
them just at the right times, just so hard, and for just so long. We carefully plan during "get set"
to act without feedback. And the action itself is a carefully orchestrated spatiotemporal
sequence, like a fireworks finale launched from a half-dozen platforms.
Unlike the roll for the player piano, which is reprogrammed only with difficulty (tape and a
punch!), the neural buffers can be reprogrammed to get the pauses right:
The notes I handle no better than many pianists. But the pauses between the notes
-- ah, that is where the art resides!
the concert pianist Artur Schnabel, 1958
So, though playing a Beethoven sonata seems quite unlike baseball, the pianist may well be using
some neural machinery that was shaped up for hammering or throwing; certainly, natural
selection hasn't acted very often on our abilities to perform music, so music is surely a spare-time
use of some such neural machinery with a crucial primary function. Dancing is a similar
secondary use, if the feet can make use of the same serial buffers that the hand needs for
throwing and hammering.
SO WHY CAN'T CHIMPS TALK if they can hammer and throw (which shows that they too
have serial buffers)? Why don't they have serial-order recreations, like music and dancing and
chess? What is it about humans that goes beyond the sufficient-for-hammering planning buffer
of the chimps? What is it that has made us so much more oriented to sequences?
Language itself is one possibility -- maybe language was so useful that natural selection selected
for the hominid variants that had better planning buffers for sentences. And then the music,
chess, and fox-trots came along as spare-time uses of the sentence sequencer. But there's another
possibility too, one that I discovered on a day like this while sitting at the beach throwing stones.
And wondering why I was so unsuccessful at hitting the targets I'd propped atop a log. I finally
moved closer so that I wouldn't have to throw so hard just to reach the log, and then I got better.
To throw twice as far with a flat trajectory, you have to throw about twice as fast. Like speeding
up a tape recording to twice the speed, you have to speed up that "motor tape" you planned and
programmed. But if I tried throwing just as hard as before from the closer position, my performance
deteriorated again. Now wasn't that interesting? It wasn't that the targets were so small when I
stood farther back; it was that I had to throw twice as fast in order to reach more distant targets.
And so I puzzled for a while about why throwing faster was so much harder than throwing
slower. Most people who have similarly puzzled over this phenomenon have probably
concluded that feedback corrections wouldn't work well when the throw was only half as long-lasting. But, as a card-carrying neurophysiologist, I knew that the feedback was always too slow;
it won't help much with even lazy throws. So if that isn't the difference between fast and twice-as-fast throwing, it must be that operating on a time scale twice as fast was a problem. Just try
dancing twice as fast as you usually dance, and you'll get the idea that adjustments aren't always
easy.
As it happened, I knew something about the problems of speeding up tape recorders, and I knew
quite a bit about how motorneurons command muscles. But I couldn't see what the problems
would be -- except for one thing: Motorneurons are inherently jittery (even at their most
constant firing rate, the interval between impulses varies a little). They can only time something
with a limited precision. Had I run into that limit, standing back too far away from the log?
There might be a half-dozen people in the world who, without having to spend a day in the
library, know the data about how jittery motorneurons are -- but I was one of them, having done
my Ph.D. thesis in 1966 on that very subject. I knew that they had great difficulty operating on a
millisecond time scale (1/1000 of a second on a camera shutter); tens of milliseconds they could
manage nicely, but their jitter kept them from timing events that required greater precision.

So how precisely did I really need to time the release of the rock from my hand when I threw
from various distances at various speeds? What's the tolerable error, the amount release time
can vary and still have the rock hit somewhere on the target? That's a simple problem in physics,
which I solved that evening after I returned home intrigued with the problem. To hit a rabbit-sized target from only 4 meters away (the length of a small car), I needed to time the release to
within 11 milliseconds (about the length of time that your camera shutter stays open when set at
1/100 of a second). That's right on the margin of what a motorneuron might be able to do by
itself. From more than 8 meters away (6 meters is a standard parallel parking space), one needed
timing precision better than 1 millisecond to consistently hit the target. So that's why I was
performing so poorly!
I felt better for a while -- until recalling that other people could perfectly well hit such targets
from much farther away than that. And so could I, once upon a time. How did we do it, if
motorneurons were so irreducibly jittery?
SCIENTISTS LOVE SITUATIONS like that: It's what we call a "problem" (actually, this was
even better; it qualified as a "paradox"), and we tend to delight in them, working them over about
like a dog gnaws on a bone from every which angle.
An engineer treats such a situation differently; he or she wants to make something that is cheap
and reliable, which can be readily fixed if it should break. The engineer treats jitter as a
nuisance, to be eliminated by better design of the parts. The scientist, on the other hand, just
wants to know why -- why the brain can manage to time something much more precisely than
any of its component parts can manage on their own. And how evolution managed to stumble
upon its method to work around the difficulty. Here is a lovely case of the whole being better
than any of its parts, but how did evolution pull it off?
Well, maybe somewhere in the brain there are neurons that are less jittery than motorneurons:
Perhaps these timing specialists just tell the motorneurons when to fire, rather than letting the
motorneurons decide for themselves? After all, for the most skilled movements (as in separating
the pages when leafing through a new book), the motor strip seems to command the
motorneurons.
Fortunately, without even spending what would have been a month in the library, I knew that
wasn't the answer either: Having recorded from those motor cortex neurons too (at least in cats
and monkeys), I knew that they were far worse than motorneurons in the amount of intrinsic
jitter, not better. Maybe somewhere else? Well, I haven't recorded from every cell type in the
brain, but I've done lots of comparative neuron physiology and I've looked at many published
records in the literature -- and I wouldn't bet on a highly precise "master clock" cell (because of
the way in which electrical events are quantized within cells, they have a lot of intrinsic jitter that
is very hard to minimize).
Yet the nervous system must, somewhere in brain or spinal cord, achieve the less-than-a-millisecond jitter: That's because we can, with practice, achieve much finer time discrimination
and movement. So, unless we are going to invoke a "soul" that commands the brain, we must try
to figure out how the nervous system pulls off this feat. It's probably like the hyperacuity
business, I thought, where we can see with finer grain than the mosaic of retinal photoreceptors.
But how?
HOW TO BUILD A PRECISE CLOCK with sloppy parts? Fortunately, I dimly remembered
from the Biophysical Journal what turned out to be a sterling example of temporal hyperacuity.
It was buried in a pile of papers atop my desk: John Clay and Robert DeHaan had done some
experiments with jittery heart cells and showed that clusters of them were much less jittery.
Your nice regular heartbeat isn't because there is some master clock with microjitter,
commanding the rest of the heart to twitch on the right beat. While there is indeed a pacemaker
region that sets the pace for the rest of the heart (it is what the vagus nerve slows down -- and
sometimes stops!), it still contains thousands of pacemaker cells, none of which is without
substantial jitter.
What Clay and DeHaan did was build a little section of heart on the bottom of a petri dish,
looking through a microscope to watch each cell twitch. A single cell in isolation beats rather
irregularly -- each heart cell is capable of serving as its own pacemaker, but its rhythm is hardly
as regular as a heartbeat. Rather than being like a water faucet's regular drip, it was more like
rain on the roof, with some pauses far longer than others.
Push a second isolated cell over until it sticks to the first; their beats, formerly independent, now
synchronize so both cells beat in synchrony. Push over a few more cells, and they too stick and
synchronize. Such "entrainment" is a primitive form of mob psychology, some say.
The funny thing is that the beat starts sounding more regular. Once you've stuck twenty-five
cells together, it's unmistakable: The jitter has dropped fivefold from what individual cells do in
isolation. With a hundred cells in the cluster, it's a tenfold reduction: Maybe not as regular as a
clock, but certainly getting to be more like a dripping faucet or a regular heartbeat. The rain-on-the-roof irregularity is gone.
The heart cells provide a nice example of the Law of Large Numbers in action, just as did the
number of cells involved in depth perception. Scientists use this mathematical principle all the
time, but with pencil and paper: We "average" a number of measurements and then calculate a
"standard deviation," which is a measure of the uncertainty or jitter. That's why public opinion
polls or estimates of the number of television viewers are bracketed: "Somewhere between 23
and 24 percent of viewers were watching the evening news." We know that to halve the standard
deviation, we need to take four times as much data; for a tenfold reduction, a hundred times as
much data. If television rating services monitored a hundred-thousand viewers simultaneously
rather than just one-thousand, they could be ten times more precise and say "23.6 percent." But
we don't usually imagine nature doing the same thing -- yet here it was, the regular rhythm of the
heartbeat being created by averaging thousands of extremely irregular beats in the individual
cells.
Now the electrical circuitry of the heart lends itself particularly well to summing up many
individual contributions and dividing by N, the number of contributions. Not all circuits of
neurons are going to do that. But the most common ones look perfectly designed for the purpose:
Individual contributions are small, many of them are summed in an "analog" fashion, and there
are a variety of ways to divide. I can think of ways for neural circuits to avoid having the Law of
Large Numbers affect their computations (all they have to do is work with a few large
contributions, an oligarchy analogous to a digital computer's binary logic), but most neural
circuits are closer to analog than binary, closer to a democracy than an oligarchy. And so most of
them are quite capable of improving on jitter by just averaging together the results of many
separate cells all trying to do the same job.
Now an engineer faced with the problem of a jittery clock usually tries to make the individual
clock more reliable -- but it is perfectly possible to achieve the same end by simply averaging
together the times of a hundred clocks. Just imagine a clock shop as midnight approaches: First
one clock starts chiming, then another and another. We just agree that when half of the hundred
clocks have begun striking the hour, we will call it midnight. Though different clocks lead the
pack on different nights, and the fiftieth clock is usually different, the interval between our
defined-by-the-fiftieth "midnights" will vary only a tenth as much as the individual clocks vary.
(Note that we are here concerned with precision and reproducibility -- not with accuracy, such
as whether it is really midnight by the time standards or whether the interval is truly twenty-four
hours).
So what do you think that evolution did: completely redesigned individual cells to make a
precision clock, or just used a lot of off-the-shelf cells hooked up in an everyday circuit? Nature
does one thing extremely well: making duplicate cells, as when a cell divides. Solving the jitter
problem by making a hundredfold extra cells may be far easier than redesigning the cell to reduce
jitter. A hundred imperfect cells rather than one perfect cell, as it were. Besides, nature seems to
like variability (its way of keeping options open) -- and apparently doesn't mind some
inefficiency or waste. Indeed, waste seems to be its key to making things better: It's what natural
selection is all about, wasting the less fit.
SO THE SOLUTION TO the throwing problem seems to be: Simply assign a multitude of serial
buffers to the same timing job. It's rather like using a hundred player pianos, all with an identical
instruction roll. Because each piano varies mechanically, the results won't be identical. It's very
much like a choir, all singing the same song: The timing of that Hallelujah Chorus refrain, when
heard in the back of the church as one fused voice, is much less jittery than the rhythmic
performance of any one singer taken alone.
Maybe that's why hominids needed a bigger brain, I thought -- they need lots more cells, just to
become hunters who throw well. Eureka?
So, how many more cells do I have to assign to the task of hitting a target that is twice as far
away? Whatever timing jitter I had at a four-meter target distance, I'll have to reduce it 8-fold to
throw twice as far. To do that with the Law of Large Numbers averaging scheme, it will take 64
times as many cells. To triple the target distance and still hit it just as reliably, I'll need 729 times
as many cells as sufficed originally. The number of cells goes up as the sixth power of the
distance -- which is indeed a steep growth curve.
Now the hominid brain has increased about fourfold beyond the apes and early hominids. Let's
see -- a 10 percent increase in cells only gains a small-brained hominid about 2 percent in
throwing distance, doubling cell numbers will buy 12 percent, and fourfold increases in cells
assigned to the timing task gains us 26 percent farther. Oops. Brain enlargement per se isn't a
simple solution to the basketball problem after all. On that reasoning, we can't even get one-third
improvements in throwing with our four-fold larger brain.
Fortunately, I finally realized, you can probably just borrow what you need as you "get set" to
throw. Cortical neurons aren't usually committed to a single task; they can be members of
different committees at different times. And so they can likely be reassigned temporarily as well
as retrained for more permanent new tasks. You just need to stop talking and stop worrying
about tomorrow and stop paying attention to anything else except throwing. On this theory,
precision throwing might involve much of frontal and temporal lobes, plus the usual basal
ganglia and cerebellum contributions. It's something like the church choir expanding temporarily
by borrowing some of the audience, getting them to sing along. You have to get them to stop
doing whatever they were doing, and instead, during "get set," assign them to the same tune as
the full-time experts in hand-arm sequencing. They may not be as expert as the pros, but -- so
says the Law of Large Numbers -- they can still be useful.
As I noted, we have had much difficulty in dissecting apart motor programs such as grooming
into the "atoms" that constitute them. Still, modular components of movements are handy for
discussing variations in plans. For simple dart throwing, you start out by cocking the elbow.
Then you contract not only the elbow flexor (biceps, etc.) but also the extensors (triceps, etc.) --
and at the same time, so that the arm doesn't actually move. This "co-contraction" serves to
stretch the elastic components of the muscles and tendons, storing elastic energy -- and it also
serves to get the extensor motorneurons all firing away, well above their thresholds for
recruitment.
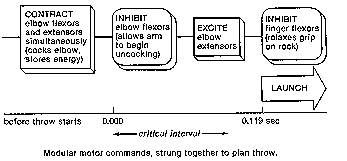
Then, to start the throw, you inhibit the flexor motorneurons so that the extensors are unopposed.
The forearm starts moving. You excite the extensors some more, in addition to inhibiting
flexors, and add to the velocity generated by the elastic rebound.
Once the forearm nears the vertical orientation, you relax your grip on the rock, probably by
simply inhibiting the finger flexors, and the inertia of the rock will serve to open the grip. It's
doing that at exactly the right moment that is so tricky (for dart throwing, it is about 119
milliseconds after the throwing movement begins uncocking the elbow).
Now you need one serial buffer for sure, just for the occasional ballistic movement like
hammering open a nut or flinging a threat. But for precision throwing, where timing jitter must
be minimized, what you'll want is many buffers all loaded up identically, marching in lockstep.
Like the choir singing the Hallelujah Chorus, you'll want to get as many extra helpers as possible:
If there are another hundred buffers that can be borrowed, so much the better -- so long as they
can quickly learn the music, i.e., can be loaded up with identical instructions. Better yet, imagine
a railroad marshalling yard, similar to the one that used to be at the end of this bike trail in the
days when it was a railroad line instead. The big parking lot at the ferry terminal probably used
to be about ten sidetracks, storing cars as they came off the railroad ferry from New York, then
making up new trains to chug up to Boston. That's essentially ten serial buffers rather like the
telephone's memories. Imagine all ten buffers loaded up with the same telephone number, all
unloading simultaneously.
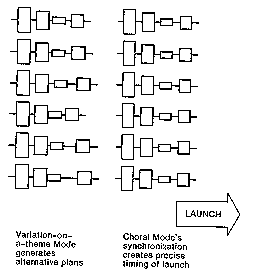 BUT WHAT ABOUT PICKING THE BEST, if it isn't a given and you have to guess? If the
occasion is a basketball free throw, and you've really "grooved" your throw (produced a standard
movement melody streamlined for the situation), then just call up your free-throw program, load
it into all the serial buffers as you get set, hook them up in lockstep, and go.
BUT WHAT ABOUT PICKING THE BEST, if it isn't a given and you have to guess? If the
occasion is a basketball free throw, and you've really "grooved" your throw (produced a standard
movement melody streamlined for the situation), then just call up your free-throw program, load
it into all the serial buffers as you get set, hook them up in lockstep, and go.
But the other reason that you need a lot of serial buffers is so that you pick the best "movement
melody" for the occasion, if it is a throw that isn't as standardized as a free throw. You call up a
whole family of variants; then, as you start to get set to throw, you judge each of them against the
situation and against memories of what worked well in similar, though not identical situations in
the past. Then go with the best -- indeed, if I were designing the system, I'd say to copy the best
one into all the other serial buffers replacing the unsuccessful candidates, then hook them all in
lockstep, and go.
In the musical analogy, it is like auditioning a series of singers, each singing a slightly different
melody; after you pick the best for this particular occasion, you photocopy her music and pass it
out to everyone else, then they all sing together as a chorus.
This step, of ganging into a chorus, is the neural networks' version of speciation in biological
evolution, and of the amplification step in the immune response. In biology, new species usually
come about because of discovering a new niche, and so a restricted number of genotypes (DNA
sequences) have a population explosion. In the immune system's use of darwinism, the sequence
of amino acids that best fits the foreign antigen undergoes a population explosion. And so the
best of the lot of the sequencing tracks in the left brain, were it replicated in the other planning
tracks for Law of Large Numbers purposes, would be similar to speciation.
Yet it isn't the exact duplications needed for throwing's submillisecond timing that are so
interesting -- it's those additional variations on the successful theme that are usually generated in
the process (just as in crossing over, and in the immune response). Shaping up a new thought --
or better yet, a poem -- through a series of "That's it! No, maybe it's even better if I say it as...."
may thus be analogous to the evolution of a whole biological lineage, one species replacing
another over and over.
MOVEMENT MELODIES are, of course, those "motor tapes" in the behavioral repertoire of the
sun-bathing cormorants of Eel Pond, and those snooping skunks. The main difference is that
ballistic movements cannot immediately utilize feedback to modify the melody; many slower
behaviors (such as cruising the waterfront for food) have such an interplay of feedback and
standard locomotion elements that they are more like jazz improvisations.
Animals that don't use varied ballistic movements don't need serial buffers. Chimpanzees and
baboons need one for hammering -- but hammering isn't that varied in its timing requirements,
so maybe they didn't have much natural selection operating on how many serial buffers they
could muster on occasion. But any animal that starts to make its living by throwing is going to
need multiple buffers for two reasons: Choosing among a family of variants (unless always
sticking to a standard throw at a standard distance), and assembling a choir and helpers for those
Hallelujah Chorus occasions that demand the most precise timing in rock release. What's nice is
that the need for a precision mode may incidentally "buy" you the wide family of choices.
When one starts thinking about thinking in a sequence, I believe the brain plays
a game -- some parts providing the stimuli, the others the reactions, and so on.
It is really a multi-person game, but consciously the appearance is of a one-dimensional, purely temporal sequence. One is only consciously aware of
something in the brain which acts as a summarizer or totalizer of the process
going on and that probably consists of many parts acting simultaneously on each
other....
the Polish mathematician Stanislaw M. Ulam, 1976



 BUT WHAT ABOUT PICKING THE BEST, if it isn't a given and you have to guess? If the
occasion is a basketball free throw, and you've really "grooved" your throw (produced a standard
movement melody streamlined for the situation), then just call up your free-throw program, load
it into all the serial buffers as you get set, hook them up in lockstep, and go.
BUT WHAT ABOUT PICKING THE BEST, if it isn't a given and you have to guess? If the
occasion is a basketball free throw, and you've really "grooved" your throw (produced a standard
movement melody streamlined for the situation), then just call up your free-throw program, load
it into all the serial buffers as you get set, hook them up in lockstep, and go.